七阶魔方花样：5x5 数独

之前有一段时间特别喜欢玩魔方，从二阶到七阶，在桌子上摆了长长的一排。后来听说九阶和十一阶也有卖的了，心中甚是痒痒，可惜囊中羞涩啊。

特别喜欢高阶魔方的一个原因，就是它们每个面上的小方格数很多（就像人们都喜欢高分辨率的显示屏一样），可以玩的花样也就多了很多。今天分享一下我的一个七阶魔方花样作品：混乱中的秩序——五阶数独。

看一看照片，你能发现其中的规律么？

七阶魔方花样（你能看出其中的规律么？）

如果边角处看不清楚，那再来看看六个面的特写：

七阶魔方花样，六个面特写——混乱中亦有规律

是不是有点儿意思？

规律是这样的，一个面周围一圈棱边的小方格颜色是一样的，六个面六种颜色。中间五乘五的二十五个小方格，恰好包含除了棱边之外的五种颜色，且每个颜色恰好出现五次。并且每个横行、竖列和两条对角线上的五个方格中都不出现重复颜色。这是不是跟五阶对角线数独非常像呢？

怎么设计这样的花样？关键在于，什么样的花样可以用魔方表现出来？

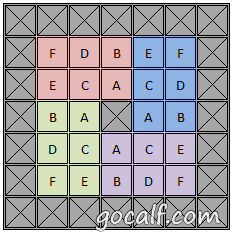
七阶魔方面块的不同位置

上面这张图是七阶魔方的一个面的示意。由于我的这个花样方案中不用考虑棱块和角块，再除去不会动的面心，剩下的 24 个方格由于旋转对称性可以分成四个等价的分区（图中用四种颜色表示）。每个分区中都有六个不同的位置，用不同的字母表示。根据魔方的运动规律，不同字母位置的方块是永远都不会互换的，就是说字母 A 永远不会跑到其他字母所在的位置去；但是任意两个（也可以是不同面的）相同字母位置的方块都是可以互换的（只考虑颜色的话，可以做到互换后不改变任何其他方块）。每个面都有六种不同的字母，每个字母出现四次。因此只要设计出来的花样满足：“每个字母在六个面中总共对应 4 * 6 = 24 个方格，在这些方格中每种颜色都恰好出现 4 次”，那这种花样就一定可以转的出来。

接着来设计花样，先找一个五阶对角线数独的分布，用下面这段随意写出的 Python 代码就可以搞定。

def FillBoard(board, n, xy):
  x = xy % n
  y = xy // n
  if y >= n:
    print('Find a possible solution.')
    return True

  existValues = set()
  existValues = existValues.union([board[y][xx] for xx in range(n)])
  existValues = existValues.union([board[yy][x] for yy in range(n)])
  if x == y:
    existValues = existValues.union([board[xx][xx] for xx in range(n)])
  if x + y == n - 1:
    existValues = existValues.union([board[xx][n-xx-1] for xx in range(n)])

  validValues = [v for v in range(1, n+1) if v not in existValues]

  if not validValues: return False
  for v in validValues:
    board[y][x] = v
    if FillBoard(board, n, xy+1): return True
    board[y][x] = None
  return False

def GenerateBoard(n):
  board = [[None for x in range(n)] for y in range(n)]
  if not FillBoard(board, n, 0):
    print('No solution.')
  return board

cnt = 5
board = GenerateBoard(cnt)

用程序找到第一组解是：

[1, 2, 3, 4, 5]
[2, 4, 5, 3, 1]
[5, 3, 2, 1, 4]
[3, 1, 4, 5, 2]
[4, 5, 1, 2, 3]

下面来确定每个数字在每一面所对应的颜色。首先六个面的面心是不能动的，因此每个面的 2 号颜色就都确定了。接着要考虑每个面的底色（就是棱块和角块的颜色），这个颜色不能随便选，要考虑魔方六个面的位置关系。我所选定的方案是，面心色蓝、红、绿、橙、黄、黑分别的对应于棱角色黑、蓝、黄、绿、橙、红。最后给每个面分配第 1、3、4、5 号颜色，稍微注意一下限制条件就好了。最后得到六个面的配色方案（程序中的 W 对应于黑色）：

def ApplyColor(board, colors):
  newboard = [[colors[v] for v in row] for row in board]
  return newboard

def DrawBoard(board):
  for row in board:
    print(row)

allcolors = (
  ['B Center', 'R', 'B', 'O', 'W', 'Y'],
  ['R Center', 'G', 'R', 'B', 'W', 'Y'],
  ['G Center', 'O', 'G', 'R', 'W', 'Y'],
  ['O Center', 'G', 'O', 'B', 'W', 'Y'],
  ['Y Center', 'R', 'Y', 'O', 'B', 'G'],
  ['W Center', 'R', 'W', 'O', 'G', 'B'],
  )
for colors in allcolors:
  print('Colors:', colors)
  colorboard = ApplyColor(board, colors)
  DrawBoard(colorboard)
  print()

最后一步就是纯体力活——转魔方。这里就不详细说了，基本的过程是先把棱块和角块转好，最后就可以随意调换每个面中部的颜色了。因为图案看起来乱乱的，转的时候很容易忘记哪边已经转好哪边还没转，只能是小心仔细慢慢进行。

So what do you think? Did I miss something? Is any part unclear? Leave your comments below.

Comments

七阶魔方花样：5x5 数独

Comments

Published

Category

Tags

Stay in Touch