最近工作忙,没时间思考复杂的问题了。正好要招人就得有面试的嘛,自己也温习一下,要不然怎么去问别人。
今天复习一下二叉树的遍历,前序(pre-order,NLR)、中序(in-order,LNR)、后序(post-order,LRN)、层序(level-order),用和不用递归。
概念就不用多解释了,前、中、后是指根结点的访问时机,在左、右子树之前、中间、或之后。层序就是从根结点开始从上至下、从左到右地依次访问。
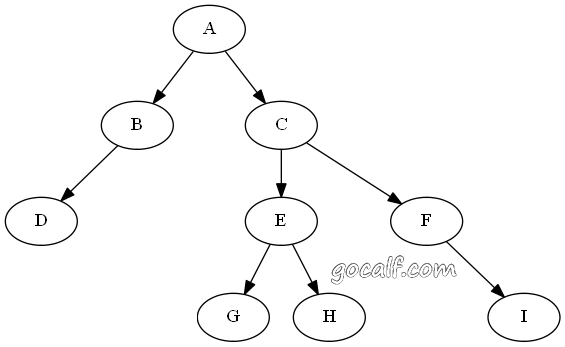
一棵二叉树
如上图所示的一棵二叉树,对应的遍历结果分别是:
- 前序(NLR):A B D C E G H F I
- 中序(LNR):D B A G E H C F I
- 后序(LRN):D B G H E I F C A
- 层序:A B C D E F G H I
一、用递归处理二叉树的前序、中序和后序遍历
递归真是一个迷人东西,它可以把复杂的逻辑变得异常简洁,这也是自然界的表现形式之一。基于递归的前、中、后序遍历二叉树的程序几乎完全相同,用两个递归调用分别处理左、右子树,剩下的事情就是打印根结点。为节省篇幅,直接把三个程序写在一起,用一个参数来控制是哪种遍历方式,也可以更方便地看出三者之间的区别。
1 2 3 4 5 6 7 | def VisitTree_Recursive(root, order):
if root:
if order == 'NLR': print(root.data)
VisitTree_Recursive(root.left, order)
if order == 'LNR': print(root.data)
VisitTree_Recursive(root.right, order)
if order == 'LRN': print(root.data)
|
二、非递归的前序、中序遍历
如果不用递归呢?实际上我们要做的就是自己维护一个栈(数据结构)来保存需要但尚未来得及处理的数据。
前序和中序都是非常简单的,当遇到一个非空的根结点时,打印其数据(如果是前序遍历),并将其压栈,然后递归地(这里用循环来模拟递归)处理其左子结点;当没有左子结点时,从栈中弹出之前遇到的某个根结点(它没有左子结点,或者左子结点已经处理完毕,需要再处理右子结点),打印数据(如果是中序遍历),然后继续处理右子结点。同样地,把两种遍历方式写在一起以便比较。
1 2 3 4 5 6 7 8 9 10 11 | def VisitTree(root, order):
s = []
while root or s:
if root:
if order == 'NLR': print(root.data)
s.append(root)
root = root.left
else:
root = s.pop()
if order == 'LNR': print(root.data)
root = root.right
|
三、非递归的后序遍历
后序遍历要稍微复杂一点点,在前序和中序遍历的程序中,当我们准备进入根结点的右子树时,根结点就被扔出栈外了。但在后序遍历时,我们仍需保留它,直到右子树处理完毕。
首先想到的改动就是在上面的程序的第 9 行到 11 行,不要从栈 s 中将根结点弹出,而是直接开始处理右子结点。但这就会带来一个问题:什么时候弹出根结点?实际上当左子树遍历完成、或者右子树遍历完成时,我们都会在栈里看到根结点,为了区分这两种状态,添加一个临时变量记录前一次访问的结点,如果前一个结点是根结点的右子树,就说明左右子树全都遍历完成了。非常简单。
1 2 3 4 5 6 7 8 9 10 11 12 13 | def VisitTreeLRN(root):
s = []
pre = None
while root or s:
if root:
s.append(root)
root = root.left
elif s[-1].right != pre:
root = s[-1].right
pre = None
else:
pre = s.pop()
print(pre.data)
|
四、非递归的层序遍历
层序遍历可以写成递归吗?还真没研究过。非递归的时候,层序遍历使用的是队列,而非栈。
处理过程非常简明,遇到一个结点,打印信息,然后依次将左、右子结点加入队列等待后续处理。
1 2 3 4 5 6 7 8 9 10 | from collections import deque
def VisitTree_LevelOrder(root):
if not root: return
q = deque([root])
while q:
root = q.popleft()
print(root.data)
if root.left: q.append(root.left)
if root.right: q.append(root.right)
|
附录
上面的 python 代码基于 v2.7。另外可以用下面这段代码来定义最简单的二叉树结点类,生成最上面图示的二叉树:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | class Node:
def __init__(self, data, left = None, right = None):
self.data = data
self.left = left
self.right = right
g = Node('G')
h = Node('H')
e = Node('E', g, h)
i = Node('I')
f = Node('F', None, i)
c = Node('C', e, f)
d = Node('D')
b = Node('B', d)
a = Node('A', b, c)
root = a
|
Comments
So what do you think? Did I miss something? Is any part unclear? Leave your comments below.