这次的题目跟二分搜索有关,如果还不能写出正确的二分搜索,那就先找出课本温习一下吧。
问题描述:给定一个由 n 个各不相等的元素构成的循环有序数组(Circularly Ordinal Array),用 O(log n) 时间、O(1) 辅助空间在其中查找指定的元素。
所谓循环有序数组,就是把一个排好序(以升序排列为例)的数组从某个(未知)位置处截为两段,把前一段放到后一段的后面,所得到的数组。比如 {8, 9, 10, 0, 1, 2, 3, 4, 5, 6, 7}。如果把数组首尾相接,看成一个环形,那么数组就还是有序的,只不过最小值有可能在任何一个位置。从最小值开始向后,数值逐渐递增,到数组的最后一个元素时再回到第一个元素。
显然应用于普通的有序数组查找的二分算法已经无法直接使用了。如果已经知道了分界点(数组最小值或最大值)的位置,那问题就简单的多了,只要先判断一下待查元素是在分界点的左侧还是右侧,然后直接对那一侧的半个数组使用二分查找即可。
那么怎么找分界点呢?它的特点是它左边的所有元素都比它右边的元素大。借鉴二分查找的思想,首先取数组中间位置的元素,拿它跟两端的元素比较,分析出分界点是在左半边还是右半边,然后对包含分界点的那半个数组递归处理。
数组的第一个元素应该是在分界点左边最小的元素,但又不小于分界点右边的任何元素。那么如果中间位置的元素比它大,分界点就只能在中间元素的右边;反之,如果中间元素比它小,分界点就一定在左半边。由于题目中规定数组元素是个不相等的,这样的判断就足够了。
如果允许重复的元素,那就有可能遇到第一个元素与中间元素相等情况,这时需要再拿最后一个元素来比较,如果中间元素比最后一个元素大,分界点就在右半边 ;反之,如果中间元素比最后一个元素小,分界点就在左半边 (感谢 chasefornone 的提醒,这种情况下,中间元素不会比最后一个元素小)。如果还是相等呢?
看看下面这张图中的两种情况(A 和 B),显然在第一次二分处理的时候,第一个(下标 0)、中间的(下标 12)和最后一个(下标 24)元素都彼此相等,分界点却有可能在任何一边。这时候就只能分别对两半继续递归处理,时间复杂度可能会变成 O(n),空间复杂度可能会(不得不用递归或者栈来保存中间状态)变成 O(log n)。
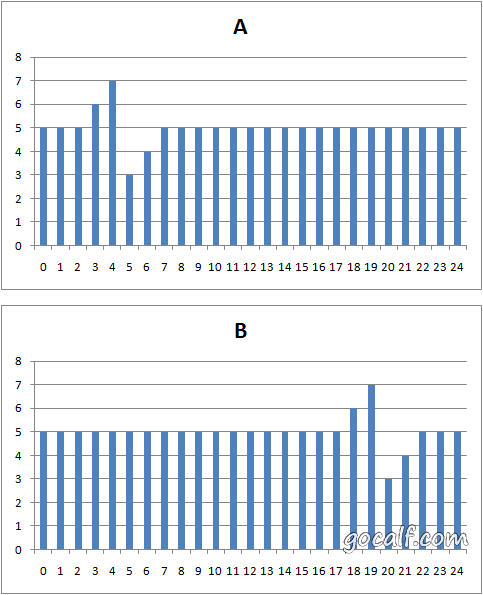
有重复元素时的特殊情况:第一个、中间的和最后一个元素彼此相等
还是简单点儿,限定元素各不相同吧……
实际上,如果仔细考量上面的寻找分界点的方法,就会发现它跟二分查找是多么的相似啊。因此另外一种方法就是将二分查找算法修改一下,相当于把找分界点跟搜索指定元素结合起来。在每次二分的时候,除了跟中间值做比较外,也要跟两端的数值做比较,以此来确定对哪一半分治处理。直接写出这种方法下的查找函数算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def CycleBSearch(arr, val):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) / 2
if val == arr[mid]:
return mid # found val
if arr[left] <= arr[mid]:
if arr[left] <= val < arr[mid]:
right = mid - 1 # val is in left side
else:
left = mid + 1 # val is in right side
else:
if arr[left] > val > arr[mid]:
left = mid + 1 # val is in right side
else:
right = mid - 1 # val is in left side
return -1 # cannot find val
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | #include <functional>
using namespace std;
template <class RandomAccessIterator, class T>
RandomAccessIterator CycleBinarySearch(RandomAccessIterator first,
RandomAccessIterator last,
const T& value)
{
return CycleBinarySearch(first, last, value, less<T>());
}
// A value, 'a', is considered equivalent to another, 'b', when
// (!comp(a, b) && !comp(b, a)).
template <class RandomAccessIterator, class T, class Compare>
RandomAccessIterator CycleBinarySearch(RandomAccessIterator first,
RandomAccessIterator last,
const T& value,
Compare comp)
{
RandomAccessIterator left = first;
RandomAccessIterator right = last - 1;
while (left <= right)
{
RandomAccessIterator mid = left + (right - left) / 2;
if (!comp(value, *mid) && !comp(*mid, value))
{
// find value
return mid;
}
if (!comp(*mid, *left))
{
if (!comp(value, *left) && comp(value, *mid))
{
// value could be in left side
right = mid - 1;
}
else
{
// value could be in right side
left = mid + 1;
}
}
else
{
if (comp(value, *left) && comp(*mid, value))
{
// value could be in right side
left = mid + 1;
}
else
{
// value could be in left side
right = mid - 1;
}
}
}
// cannot find value
return last;
}
|
话说我还是更喜欢 Python 啊。
Comments
So what do you think? Did I miss something? Is any part unclear? Leave your comments below.