时针，分针，相对运动

注意：本文涉及到的是小学、初中级别的问题，请高智商同学自动绕行。

不知道为什么，我从小就对时钟感觉到头疼，类似于时针、分针在什么时刻重合、什么时候成九十度角之类的问题尤其感到无从下手。今天这篇文章用来纪念懵懂的曾经。

感谢 Chunxu 同学提供的题目：

某人 6 点多从家出发，出门时时针和分针是 110 度角，7 点前回到家，时针和分针还是 110 度角。问这人出门多久？

这个问题非常简单，设出门时间是 6 点 x 分，回家时间是 6 点 y 分，根据时针分针的旋转速度列出方程，联列求解，最后求出 y-x 便是答案。

然而更简单的方法是借助于相对运动。分针每小时转一圈，其转速为 6 度/分；时针 12 小时转一圈，转速为 0.5 度/分。所以相对于时针而言，分针的转速是 6 - 0.5 = 5.5 度/分。根据题目，出门的时候分针比时针落后（顺时针方向为前方）110 度，而回家时超前时针 110 度，那么相对于时针，分针一共转了 220 度。因此经过的时间就是 220 / 5.5 = 40 分钟。

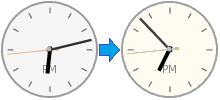
6:12:44 至 6:52:44 是此人回家路上所经历的时间段

用类似的方法求解时针与分针的重合时刻也是非常简单的。比如问四点到五点之间，分针何时与时针重合。因为四点整的时候分针在时针后面 120 度，当二者重合时，分针相对于时针旋转了 120 度，耗时 120 / 5.5 = 21 分 49.09 秒。所以重合的时刻是 4 点 21 分 49.09 秒（如下图示）。

据说微软也曾经拿时针、分针、秒针当过面试题，这东西确实非常简单，但有时候也确实挺让人头疼的。希望以后不会再被类似的问题困扰。

Like this post? Share on: Twitter ❄ Facebook ❄ Email