前几天在 Matrix67 的博客里看到了这个益智小游戏:Manufactoria,抽空玩了玩,虽然关卡不算多,但非常有趣。
这是个程序设计类的游戏,感觉就像是个状态机吧(有限自动机?),从纸带上读取数据,具有分支和写数据的功能,利用简单的几种元件组装成一台可以识别特定模式或者完成指定运算的机器。
游戏的背景大概是一家工业机器人(Industrial Robotics)生产厂请你(机器人工程师,Robotics Engineer)来测试和修复他们制造的机器人,所谓的“测试”就是对机器人内部纸带上的红蓝色点进行检测,判断其是否满足指定的模式;“修复”就是对纸带上的红蓝色点进行处理或者运算,产生指定的结果。这个游戏还支持自定义关卡,看到过有人提出求最大公约数之类的问题。
不知道别人是怎么思考的,反正我是先画想好用什么算法,然后在纸上画状态图把细节尤其是边界条件考虑清楚,然后开始布局,通过验证之后再不断地优化(减少使用的元件数量)。
开头几关非常简单,玩了七八关之后,每开启新的一关就在想,这怎么可能实现啊,但解决了之后又发现其实很简单。主要还是开始没有适应它的这种工作方式吧。
我的建议是每个程序员都应该玩一下这个游戏,我甚至考虑可以把它用在第一轮面试上,跟 candidate 随便聊聊天,让他玩一两关看看他的思路如何。
Matrix67 的这篇博客是一年多之前发的了,后来我又找到了这个游戏的 官方网站(http://pleasingfungus.com/#!/Manufactoria),发现游戏版本更新了,细节上有不少改进,增加了不少测试用例,统计出来的运行时间也有所变化(另外要注意的是,在新版本中如果想让两个传送带正交于某个方格,需要按 Shift 键,否则就会替换)。
(如果上面的 Flash 无法加载,可以尝试我在这里上传的:Manufactoria.swf。)
分享一下我在各关的解法(进入一个关卡,点击磁盘图标,在文本框中粘贴解法代码即可;注意贴入的代码中的关卡序号不需要与当前所在的关卡序号一致,游戏会自动跳转到正确的关卡,除非你还没有激活那一关)。另外很多关卡都有无数种解法,我一般会尽量优化使之元件个数最少(比较测试时间没有太大意义,一旦下一个版本的测试用例变化,测试时间就不一样了)。
下面这张图是游戏当前版本(v1.30)的关卡分布图,为了方便查找,我特意用红色字体添加了关卡序号在每关图标的左上角处。其中第 29 到 31 关是隐藏关,要通过了第 24 关才能显示出来。
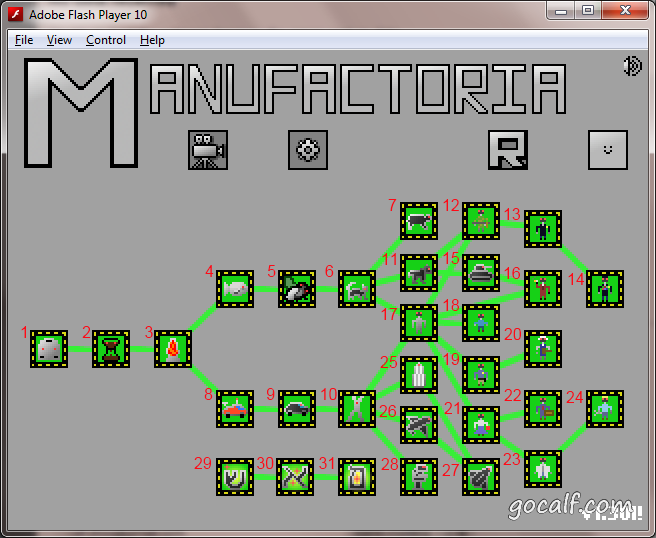
Manufactoria 主界面(添加了关卡序号)
我的各关卡解决方案(第 30 和 31 关没有时间优化了,其他关都是尽可能优化过的):
?lvl=1&code=c12:6f3;c12:7f3;c12:8f3;
?lvl=2&code=c12:8f3;p12:6f2;c12:7f3;
?lvl=3&code=p12:5f3;c13:5f0;p11:6f2;c11:5f3;p11:8f2;c11:7f3;c11:9f3;c11:10f2;
?lvl=4&code=p12:6f3;c11:6f2;c12:7f3;c12:8f3;
?lvl=5&code=p12:4f3;c12:6f3;c12:7f3;c12:8f3;c12:9f3;c12:10f3;p11:4f6;p13:4f4;p11:5f6;p13:5f4;c12:5f3;
?lvl=6&code=c12:4f3;p12:5f2;p12:6f2;c12:8f3;c12:9f3;c12:10f3;p12:7f7;c13:7f0;c11:7f1;c11:6f1;c11:5f2;
?lvl=7&code=c12:8f3;c12:9f3;c12:10f3;c11:3f3;c11:6f1;c12:5f3;c12:6f3;c13:3f3;c13:6f1;c12:7f3;p12:4f3;p11:4f6;p11:5f0;p13:4f4;p13:5f2;
?lvl=8&code=p12:6f3;b11:6f3;r13:6f3;c11:7f2;c13:7f0;c12:7f3;c12:8f3;
?lvl=9&code=c12:7f3;c12:8f3;c12:9f3;p12:5f3;g11:5f2;y13:5f0;c12:6f3;
?lvl=10&code=g12:4f3;p12:5f3;b11:5f2;r13:5f0;y12:6f3;c12:7f3;c12:8f3;c12:9f3;c12:10f3;
?lvl=11&code=c12:8f3;c12:9f3;p12:5f3;p13:5f3;c11:5f2;c14:5f0;c12:6f3;c12:7f3;
?lvl=12&code=r12:4f3;r12:5f3;r12:6f3;c12:7f3;c12:8f3;c12:9f3;c12:10f3;
?lvl=13&code=c12:10f3;c12:11f3;c12:12f3;q12:2f7;y12:3f3;r12:4f2;c12:5f1;c12:7f3;c12:8f3;y13:2f0;q13:3f6;p13:4f6;q13:5f4;b13:6f3;q13:7f4;r13:8f1;b14:3f3;c14:4f0;c12:9f3;
?lvl=14&code=c12:10f3;c12:11f3;c12:12f3;q12:2f7;y12:3f3;c12:7f3;c12:8f3;y13:2f0;q13:3f6;q13:7f4;c14:4f0;c12:9f3;p13:4f2;r14:3f3;r13:6f3;b13:8f1;r12:4f2;q13:5f2;b14:5f1;
?lvl=14&code=c12:10f3;c12:11f3;c12:12f3;c12:8f3;c12:9f3;r12:4f3;p13:5f2;r13:7f3;q13:8f4;b13:9f1;b12:6f1;c12:5f2;q13:4f0;q13:6f4;q12:2f7;y13:2f0;y12:3f3;c13:3f1;
?lvl=15&code=c11:5f3;c13:5f3;c13:6f0;p11:11f3;c12:11f3;i11:12f7;c10:11f3;c10:12f2;p12:4f2;c12:3f3;c10:7f3;c10:8f2;c10:9f3;p11:7f3;c11:8f3;p11:9f3;c12:7f3;c12:8f0;c12:9f3;c12:10f0;c11:6f3;c12:6f0;c10:10f2;c11:10f3;p12:5f1;
?lvl=16&code=c12:4f3;p12:5f2;p12:6f3;c12:7f3;c12:8f3;c12:9f3;c12:10f3;p13:6f7;
?lvl=17&code=y12:4f3;c12:7f3;c12:8f3;c12:9f3;c12:10f3;p12:6f3;i12:5f7;p11:6f4;b11:7f1;p11:5f1;r10:5f2;q11:4f1;
?lvl=18&code=c10:4f2;b10:5f1;c11:4f2;p11:5f3;c12:4f3;p12:5f3;c13:4f0;p13:5f3;c14:4f0;r14:5f1;y12:3f3;q12:6f2;p12:7f3;p11:7f3;p13:7f3;y10:7f1;y14:7f1;c10:6f1;c14:6f1;c12:8f3;c12:9f3;c12:10f3;c12:11f3;
# 2024-10 @837951602 提供的更优解法:
?lvl=18&code=c10:4f2;b10:5f1;i11:4f3;c12:4f3;p12:5f3;i13:4f2;c14:4f0;r14:5f1;y12:3f3;c12:8f3;c12:9f3;c12:10f3;c12:11f3;p11:5f5;p13:5f5;y11:6f1;p12:6f3;y13:6f1;q12:7f0;g11:7f2;
?lvl=19&code=c12:10f3;c12:11f3;c12:12f3;c12:6f3;c12:8f3;c12:9f3;g12:3f3;y12:4f3;q12:5f0;i12:2f7;c12:7f3;p15:3f3;b14:3f3;r16:3f3;c16:4f0;c15:4f0;y14:4f3;c13:5f0;q14:5f7;p14:6f1;r13:6f2;b15:6f0;c9:2f2;r9:3f1;c10:2f2;p10:3f1;c10:4f1;c10:5f1;c10:6f1;c11:2f2;b11:3f1;b11:4f0;p11:5f0;r11:6f0;b13:1f2;g13:2f2;p14:1f3;q14:2f1;r15:1f0;c15:2f3;
?lvl=20&code=c12:12f3;c12:6f3;c12:8f3;c9:2f2;r9:3f1;c10:2f2;p10:3f1;c10:4f1;c10:5f1;c10:6f1;c11:2f2;b11:3f1;b11:4f0;p11:5f0;r11:6f0;g12:3f3;y12:4f3;q12:5f0;i12:2f7;g13:2f2;q14:2f1;c15:2f3;p14:1f3;b13:1f2;r15:1f0;p15:3f3;b14:3f3;r16:3f3;c16:4f0;c15:4f0;y14:4f3;c13:5f0;q14:5f7;p14:6f1;r13:6f2;b15:6f0;y12:7f3;p11:7f7;p13:7f7;c11:8f1;c13:8f1;p12:9f3;q11:9f0;q13:9f6;p10:9f2;p14:9f0;r10:8f3;r14:10f1;b10:10f1;b14:8f3;q12:10f2;q12:11f2;
?lvl=21&code=c12:7f3;c12:8f3;c12:9f3;c12:10f3;c12:11f3;c12:12f3;c12:6f3;p12:3f3;c12:4f3;c12:5f3;y12:2f3;r8:2f2;p9:2f1;p9:3f4;b9:4f1;b10:1f3;p10:2f6;i10:3f1;c11:3f0;q11:2f1;
?lvl=22&code=c12:11f3;c12:12f3;c12:9f3;c12:10f3;c10:5f2;c10:7f1;g11:2f2;p11:3f0;y11:4f1;q11:6f7;q11:8f7;p12:3f3;c12:5f3;q12:6f7;q12:8f7;y13:3f0;q13:6f7;q13:8f7;c14:5f0;c14:7f1;c12:2f3;r12:4f3;r14:8f1;r10:8f1;p12:7f0;g10:6f1;c11:5f2;c13:5f0;y14:6f1;
?lvl=23&code=c12:12f3;c12:10f3;c12:11f3;c12:9f3;p12:4f3;p10:4f2;r10:3f3;b10:5f1;p14:4f0;r14:5f1;b14:3f3;c12:8f3;c11:3f2;c13:3f0;p12:6f3;b11:6f2;r13:6f0;y12:3f3;g12:2f3;g13:5f2;g11:5f0;q13:4f6;q11:4f0;q12:5f6;q12:7f2;
?lvl=24&code=c12:9f3;c12:10f3;c12:11f3;c12:6f3;c12:7f3;c12:8f3;c12:12f3;b10:3f3;c10:4f2;r10:5f1;p11:4f6;q11:5f4;y12:3f3;p12:4f3;c12:5f3;p13:4f4;q13:5f2;r14:3f3;c14:4f0;b14:5f1;q13:3f6;q11:3f0;c12:2f3;c11:2f2;c13:2f0;
?lvl=25&code=y12:5f3;p12:6f3;r11:6f2;b13:6f0;q12:7f2;c12:8f3;c12:9f3;
?lvl=26&code=y12:5f3;p12:6f3;c13:6f0;b11:6f2;q12:7f2;c12:8f3;c12:9f3;
?lvl=27&code=c12:10f3;g12:4f3;y12:5f3;p12:6f3;b11:6f2;q13:6f6;p14:6f0;b14:5f3;c13:5f0;r14:7f1;g13:7f2;q12:7f6;p12:8f3;b11:8f2;r13:8f0;q12:9f2;
?lvl=28&code=y12:3f3;c12:9f3;c12:10f3;c12:11f3;q11:5f5;p12:5f3;q13:5f1;c12:4f3;b11:4f2;r13:4f0;y10:5f3;y14:5f3;c10:6f2;c14:6f0;b11:6f2;r13:6f0;p12:6f3;c12:8f3;q12:7f2;
?lvl=29&code=p12:5f3;c12:9f3;c12:10f3;c12:11f3;p11:3f1;c11:4f1;q11:5f4;p13:3f1;c13:4f1;q13:5f2;r10:4f3;p10:5f2;b10:6f1;b14:4f3;p14:5f0;r14:6f1;q12:6f0;q12:7f0;c12:8f3;g12:3f3;c12:4f3;
?lvl=30&code=c12:4f3;g14:5f3;q11:5f1;q13:5f5;c14:7f3;q15:8f5;q13:8f1;g12:8f3;g16:8f3;c11:9f3;c13:9f3;c15:10f0;c14:10f0;c12:10f3;c12:12f2;c13:12f2;c14:12f2;c15:12f2;c16:12f2;c17:12f2;c18:12f1;c18:11f1;c18:10f1;c18:9f1;c18:8f1;c18:7f1;c18:6f1;c18:5f1;c18:4f1;c18:3f0;c17:3f0;c16:3f0;c15:3f0;c14:3f0;c13:3f0;q12:11f7;p12:5f7;c11:6f0;c14:6f3;p14:8f3;b13:7f2;r15:7f0;q12:9f3;g13:10f0;y11:10f2;b13:4f0;r11:4f2;q12:6f7;c14:9f2;c15:9f1;q16:10f3;c16:9f3;c17:10f3;c17:11f0;c16:11f0;c15:11f1;c9:12f2;c10:11f3;p10:12f7;q10:13f3;c11:11f0;q11:13f3;c6:9f3;c6:10f2;g7:8f3;q7:9f3;c7:10f2;b8:7f2;q8:8f1;c9:5f3;g9:6f3;c9:7f3;p9:8f3;c10:6f0;r10:7f0;q10:8f5;c9:9f2;c10:9f1;c11:8f2;c8:10f2;c9:10f2;c10:10f2;c8:9f3;g12:2f0;y11:2f3;c11:3f2;c12:3f3;c10:5f0;
?lvl=31&code=c18:5f1;c18:4f1;c18:3f0;c17:3f0;c16:3f0;c15:3f0;c14:3f0;r13:2f3;g12:2f2;g13:3f0;c12:3f0;p10:3f0;c11:3f0;q10:2f2;q10:4f6;r11:4f1;b11:2f3;g10:1f0;g10:5f2;i9:4f7;b6:8f3;g7:7f3;p7:8f3;b8:6f2;q8:7f1;b8:8f3;c9:6f3;p9:7f3;c9:8f2;r10:6f0;q10:7f5;c10:8f1;c11:7f2;b11:8f3;g12:7f3;p12:8f3;b13:6f2;q13:7f1;r13:8f3;c14:6f3;p14:7f3;c14:8f2;c14:9f0;r15:6f0;q15:7f5;c15:8f1;r15:9f0;g16:7f3;c16:8f3;c9:5f3;c11:5f2;c12:5f2;c13:5f2;c14:5f3;p15:10f0;r15:11f0;c16:9f3;c16:10f0;b6:11f2;p7:11f3;q7:12f3;r8:11f0;c8:12f2;q9:12f5;c7:10f3;r14:11f1;c14:10f0;c13:10f0;c12:10f0;c11:10f0;c10:10f0;c9:10f0;c8:10f0;b13:9f3;r11:9f3;c9:11f2;c10:11f2;c11:11f2;c12:11f2;c13:11f3;i13:12f5;c13:13f2;c14:13f2;c15:13f2;c16:13f2;c17:13f2;c18:13f1;c18:12f1;c18:11f1;c18:10f1;c18:9f1;c18:8f1;c18:7f1;c18:6f1;q10:12f6;c10:13f2;c11:13f2;g11:12f2;c14:12f2;c15:12f2;c16:12f2;c17:12f1;c17:11f1;c17:10f1;c17:9f1;c17:8f1;c17:7f1;c17:6f1;c17:5f0;c16:5f0;c15:5f0;g12:12f2;r8:9f3;b6:9f3;c6:10f2;i9:3f6;c8:4f2;c9:1f3;c9:2f3;c8:3f3;
(END)
~~~~~~~~~~ 分隔符 ~~~~~~~~~~
以下内容有剧透,三思而后看。
~~~~~~~~~~ 分隔符 ~~~~~~~~~~
- Level 1: Robotoast! ACCEPT: Move robots from the entrance (top) to the exit (bottom)!
- 没有任何悬念,用 3 个元件,耗时 32764(注意这是 v1.30 里的计时单位,在老版本中大概是 0:02)。
- Level 2: Robocoffee! If a robot's string starts with blue, accept. Otherwise, reject!
- 要求接受以蓝色开头的机器人。也没有任何可以商量的,3 个元件,耗时 24572。
- Level 3: Robolamp! ACCEPT: if there are three or more blues!
- 要求接受纸带中有至少 3 个蓝点的机器人。8 个元件,112570 时间。
- Level 4: Robofish! ACCEPT: if a robot contains NO red!
- 要求接受没有红点的机器人。4 个元件,32764 时间。
- Level 5: Robobugs! ACCEPT: if the tape has only alternating colors!
- 如果纸带上的颜色是交替出现的(没有连续的红色或蓝色)就接受。6 个元件,32900 时间。
- Level 6: Robocats! ACCEPT: if the tape ends with two blues!
- 如果最后两个颜色是蓝色则接受。11 个元件,182272 时间。
- Level 7: Robobears! ACCEPT: Strings that begin and end with the same color!
- 如果第一个和最后一个色点颜色相同则接受。注意没有色点和只有一个色点这两种特殊情况。15 个元件,176136 时间。
- Level 8: RC Cars! OUTPUT: The input, but with the first symbol at the end!
- 把第一个色点放到最后去。7 个元件,49144 时间。
- Leve 9: Robocars! OUTPUT: Replace blue with green, and red with yellow!
- 把蓝色和红色分别换成了绿色和黄色。7 个元件,229374 时间。
- Level 10: Robostilts! OUTPUT: Put a green at the beginning and a yellow at the end!
- 在色带的最前端放一个绿色,末尾处放一个黄色。毫无悬念,9 个元件,53244 时间。
- Level 11: ACCEPT: With blue as 1 and red as 0, accept odd binary strings!
- 只接受奇数数字,也就是最后一位是蓝色的。至于空色带就无所谓了,严格来讲应该是不接受,但至少这个版本里没有这样的测试数据。8 个元件,167931 时间。
- Level 12: Soldiers! OUTPUT: With blue as 1 and red as 0, multiply by 8!
- 要把输入的数字乘以 8,程序员对这个应该是得心应手了,再末尾添加三个 0(红色)即可。7 个元件,65520 时间。
- Level 13: Officers! OUTPUT: With blue as 1 and red as 0, add 1 to the binary string!
给输入的数字做加 1 操作。开始的时候感觉是无法完成的,但仔细想想就很简单。加 1 操作,从二进制的角度来看,就是把末尾的 1 都变成 0,最后一个 0 变成 1。主要的难点是要从最后一位往前加,所以要不端地循环,每次都处理最后一个没有处理过的色点。另外在优化的时候发现,可以先把末尾的 1 变成黄色,这样就不需要再另外使用分隔符号了。分隔符用来标记字串的中止以及当前处理到的位置。
19 个元件,81580 时间。
- Level 14: Generals! OUTPUT: Substract 1 from the binary string! (Input>= 1)
减 1 操作,跟第 13 关其实是一样的,红色和蓝色互换就好了。19 个元件,79750 时间。
但这一关还可以再稍微调整一下布局,变成 18 个元件,81686 时间。
- Level 15: Robotanks! ACCEPT: With blue as 1 and red as 0, accept binary strings > 15!
- 要求接受大于 15 的数字。也就是要求大于或等于 16,即 1 后面至少有四个二进制位。于是就是要判断第一个蓝色后面是否至少有四个色点,不论颜色。25 个元件,19958 时间。
- Level 16: Robospies! ACCEPT: With blue as 1 and red as 0, accept natural powers of four!
- 要求接受 4 的幂,也就是第一个蓝色后面必须恰好有偶数(包括 0)个红色色点。注意要忽略掉开头的红色。8 个元件,57372 时间。
- Level 17: Androids! ACCEPT: Some number of blue, then the same number of red!
- 要求纸带上的色点必须是若干个蓝色后面跟着同样数量的红色。开始也是觉得很难,主要是没有办法计数。当然解决办法就是一次一次循环,每次循环中判断一对红蓝色点。对于这种需要循环处理的问题,我一般都用一个黄色作为分隔符作为字符串的终结标记。12 个元件,63041 时间。
- Level 18: Robo-children! ACCEPT: An equal number of blue and red, in any order!
判断色带上蓝色和红色的数量是否恰好相等。依旧是每次循环检查一对。23 个元件,266582 时间。
PS:2024-10 @837951602 在评论中提供了一个更优的解法,只用 20 个元件。
- Level 19: Police! OUTPUT: Put a yellow in the middle of the (even-length) string!
输入的色带上有偶数个色点(不用判断是否满足),要求在中间位置插入一个黄色。这一关开始想了好久,排满了整个棋盘才搞定,后来一直优化到 40 个元件。想到了两种方案,一种是在颜色串的首尾各放一个色点,每次循环的时候让两个色点分别向中间移动一格,直到二者相遇。另一种是用起始位置放两个色点,每次循环的时候一个色点往后移动一格,另一个色点往后移动两个。我最后的优化版是采用第二种方法的。40 个元件,291584 时间。
如果输入的色带上有奇数个色点,那我的算法会在中间色点的后方插入黄色。
- Level 20: Judiciary! ACCEPT: (Even-length) strings that repeat midway through!
判断色带上的色点(偶数个)是否恰好前半部分与后半部分的排列完全一样。比如如果前半部分是红蓝红红蓝,后半部分也必须是红蓝红红蓝。这一关我是直接利用了第 19 关和第 29 关(恰好我是先完成了第 29 关才回过头玩的这关),即先给这个颜色串的中间位置添加一个黄色(直接照搬第 19 关的布局),然后利用第 29 关的布局判断黄色分割的两个子串是否完全一致。
52 个元件,319428 时间。
- Level 21: Teachers! ACCEPT: X blue, then X red, then X more blue, for any X!
要求色带上恰好是有若干个蓝色,跟着同样数目的红色和另外同样数目个蓝色。也可以是一个色点都没有。跟第 17 关的算法完全一样,只要再考虑考虑布局即可。
20 个元件,76590 时间。
- Level 22: Politicians! ACCEPT: If there are exactly twice as many blues as red!
判断色带上蓝色是否恰好是红色的两倍。这一关其实跟第 18 关没有太大区别,一个简单高效的解决办法就是先把蓝色减半,然套用第 18 关的布局来检测减半后的蓝色是否与红色数目相等。
给蓝色减半的时候,比较传统的办法是用一个黄色作为色串终止符,从头开始,每读到一个红色就写一个红色,读到两个蓝色之后写一个蓝色。或着稍微变化一下,不用额外的黄色作终止符,而是在遍历的时候直接用黄色替换红色,用一个绿色替换两个蓝色。
用 29 个元件,296870 时间。
- Level 23: Academics! OUTPUT: Reverse the input string!
把输入的颜色串反转。基本的方法就是把第一个色点放到色串的最后,再把第二个色点放到倒数第二位。除了用一个黄色标记色串的终止外,在用一个绿色分割尚未处理的色串和部分反转了的色串。
用 25 个元素,227328 时间。
- Level 24: Engineers! ACCEPT: Perfectly symmetrical strings!
- 判断颜色串是否是对称的。也比较简单啦,每次用第一个色点做分支,在每个分支里判断最后一个色点,如果跟第一个一样则继续,否则丢弃。用 25 个元件,47696 时间。
- Level 25: Roborockets! OUTPUT: Swap blue for red, and red for blue!
- 把红蓝颜色互换。毫无悬念,7 个元件,229374 时间。
- Level 26: Roboplanes! OUTPUT: All of the blue, but none of the red!
- 保留输入中的所有蓝色,丢掉红色。跟第 25 关唯一的区别就是遇到红色后不再写回到色带上。7 个元件,22526 时间。
- Level 27: Rocket Planes! OUTPUT: The input, but with all blues moved to the front!
把输入中的蓝色都移动到红色的前面。
这一关有点儿意思,我最后设计的方法是直接利用第 23 关反转输入的方法。在第 23 关的布局中,中轴线左边是针对第一个是蓝色的处理,右边是针对第一个是红色的处理。在这一关里依旧保留右半边,但把左半边改成遇到蓝色就直接写一个蓝色回去。最后的效果就是不断地把红色往最后写,直到红色全都聚集到后半部分。
用 16 个元件,12390 时间。
- Level 28: Robomecha! OUTPUT: The input, but with the last symbol moved to the front!
- 把最后一个色点放到最前面。很简单,19 个元件,606214 时间。
- Level 29: Seraphim! ACCEPT: Two identical strings, separated by a green!
- 判断由绿色点分开的两个色串是否完全相等。也挺简单的,补一个绿色作为终止符,取出色串一的第一个颜色,把其他的写回纸带,判断色串二的第一个颜色跟它是否一样;这时候两个色串都去掉了第一个颜色,而且刚好色串二跟色串一交换了顺序,再重复用同样的方法判断下去即可。21 个元件,166182 时间。
- Level 30: Ophanim! ACCEPT: Read the tape as two numbers, A and B, split by a green: accept if A > B!
由绿色点分开的两个色串,从二进制数字的角度判断是否前一个数大于后一个数。
我用的方法是求 B - A,当然不用记录完整的结果,只要记录借位状态即可。不过我没有再进行优化,现在用了 88 个元件,60617 时间。估计能优化掉一小半的元件。
- Level 31: Metatron! OUTPUT: Read the tape as two numbers, A and B, split by a green: output A + B!
- 计算被绿色分开的两个数字之和。基本上就是从最低位逐位加上去。同样是还没有优化,应该能减少一半以上的元件。现在用 120 个元件,108630 时间。
Comments
So what do you think? Did I miss something? Is any part unclear? Leave your comments below.